 |
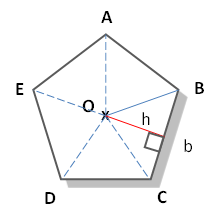
O = le centre du pentagone régulier ABCDE h = la hauteur du triangle CÔB b = longueur de chaque côté du polygone régulier ABCDE |
L’aire du polygone régulier est égale à la somme de l’air des 5 triangles isométriques qui le composent :
| Aire du pentagone régulier = | 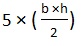 |
Un pentagone régulier est une figure géométrique dont les 5 côtés sont de même longueur.
Le pentagone régulier fait donc partie des polygones (figures à plusieurs côtés) réguliers.
 |
On notera que cette formule peut s’utiliser pour le calcul de n’importe quel polygone régulier. Il suffira de remplacer dans la formule 5 par le nombre de côté du polygone. |
Apothème : Un apothème désigne la ligne la médiatrice du côté d'un polygone régulier, qui est aussi le rayon du cercle inscrit au polygone.
ABCDE est un pentagone régulier dont la longueur de chaque côté est de 6 cm.
Soit b, la longueur de l’apothème égale à 4,9 cm.
Aire du pentagone régulier ABCDE = 5 x (6 x 4,9) / 2 = 73,5 cm²