Homothétie

Définition de l'homothétie

Soit un point O et un réel stritement positif k.

L'homothétie h de centre O et de rapport k associe à tout point M le point M' tel que OM' = k OM, et tel que si M différent de O, M' appartient à la demi-droite [OM).

On dit que M' est l'image de M par l'homothétie h de centre O et de rapport k.

Prenons un exemple

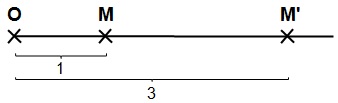
Dans l'exemple ci-dessous, M' est l'image de M par l'homothétie h de centre O et de rapport 3. En effet, dans notre cas OM' = 3 OM.

Propriétés des homothéties

Les homothéties de rapport k > 0 multiplient les distances par k :

• - Si k > 1, l'effet d'une homothétie de rapport k sur une distance est celui d'un agrandissement.
• - Si 0 < k < 1, l'effet d'une homothétie de rapport k sur une distance est celui d'une réduction.

Image d'une droite par une homothétie

L'image d'une droite par une homothétie h est une droite qui lui est parallèle.